人工智能知识表示：谓词逻辑在考试重点1~4章中的应用与解析

考试范围：第1〜4章

知识点记忆

门户网站

第2章知识表达

有以下语句，请使用相应的谓词公式表达它们：

（1）有些人喜欢李子花，有些人喜欢菊花，有些人喜欢李子花和菊花

p（x）：x是人类

l（x，y）：x像y

其中，Y的单个领域是{李子花，菊花}。

（∃x）（p（x） - > l（x，李子开花）v l（x，chrysanthemum）v（l（x，plum blossom）∧l（x，chrysanthemum）））））））

（2）有些人每天下午去打篮球。

p（x）：x是人类

B（X）：X打篮球

a（y）：y是下午

（∃X）（∀Y）（a（y） - > b（x）∧P（x））

∧优先级高于 - >

（3）新计算机很快并且具有较大的存储容量

NC（X）：X是一种新型计算机

f（x）：x快速b

B（x）：x大容量

（∀x）（nc（x） - > f（x）∧B（x））

（4）并非每个计算机学生都喜欢在计算机上编程程序

S（X）：X是计算机系的学生

l（x，pragramming）：x喜欢编程

U（X，计算机）：X使用计算机

¬（∀X）（s（x） - > l（x，pragramming）∧U（x，Computer））

（5）喜欢编程的人喜欢计算机

p（x）：x是人类

l（x，y）：x像y

（∀X）（p（x）∧L（x，pragramming） - > l（x，Computer））

（1）使用谓词表示解决机器人的构建块问题。假设机器人有一只机器人手，并且要处理的世界有一个桌子，并且可以将几个相同的正方形构件堆叠在桌子上。机器人有四个典型的操作构建块的典型动作：从桌子上捡起一个构建块；将构件放在桌子上；在构建块上拿起一个构建块。图中显示了构建块世界的布局：

（1）首先定义谓词

清除（x）：构建块X为空

在（x，y）上：构建块X在构件上y

安排（x）：构建块x在桌子上

握住（x）：机器人抓住x

手工：机器人是空的

x，y的单个域是{a，b，c}

从图片中，初始状态：

安排（a）

安排（b）

在（c，a）上

清除（b）

清除（c）

目标状态：

安排（c）

在（b，c）上

在（a，b）上

清除（a）

手工

（2）定义描述操作的谓词

拾音器（x）：从桌面x拿起一个街区

Putdown（x）：将构件放在桌面上

堆栈（x，y）：将一个块y堆放在块x的顶部

上市（x，y）：从块x拿起一个街区y

每个操作都可以分为两个部分：条件和动作

皮卡（x）

条件：安排（x），手工，清除（x）

动作：删除表：安方（x），hingempty

------------添加表：手工（x）

putdown（x）

条件：手工（x）

操作：删除表：手工（x）

-----------添加表：安装（x），清除（x），手工

堆栈（x，y）

条件：手工，清晰（y），on（y，x）

操作：删除表：手工，在（y，x）上

-----------添加表：保留（y），清除（x）

堆场（x，y）

条件：手工，清晰（y），on（y，x）

操作：删除表：手工，在（y，x）上

-----------添加表：保留（y），清除（x）

我不知道这段是否需要

（3）解决问题的过程

（2）使用谓词表示来解决僧侣和野蛮人的问题。在河的北岸有三名和尚，三个野蛮人和一条船。僧侣想用这艘船运送所有人，但要遵守以下条件：

僧侣和野蛮人可以划船，但船只一次只能在任何海岸上运送两个人。野蛮人的数量不能超过僧侣的数量，否则僧侣将被野蛮人吃掉。

如果野蛮人愿意遵守任何形式的交叉安排，清单计划确保僧侣的安全，要求所有谓词的各个领域写作。

可能是过程

请在语义网络中表达以下命题

（1）树木和草是植物

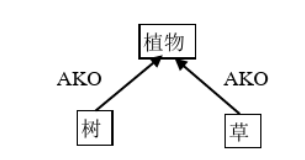
（2）树木和草有根源

（3）水生植物是草，生活在水中

（4）果树是一棵树，会带来果实

请为以下命题编写他们的语义网络

（1）GAO老师从7月至8月向计算机学生教授“计算机网络”课程

（2）创新公司位于Kehai Street 56号。 Liu Yang是公司的经理。他今年32岁，拥有硕士学位。

（3）红队和蓝队参加了一场足球比赛，得分为3：2

（1）假设有以下天气预报：“北京在今天的白天晴天，北风为3级，最高温度为12度，最低温度为-2度，降水的可能性为15％。请使用框架来表达这一知识。

 frame<天气预报>
 	地域：北京
 	时段：今天白天
 	天气：晴
 	风向：偏北风
 	风力：3级
 	气温：最高：12度			
 	      最低：-2度
 	降水概率：15%

（2）以“教师学生框架”，“教师框架”和“学生框架”的形式编写系统描述

 师生框架
 Frame< Teachers-Students >
 	Name: Unit (Last-name, First-name)

 	Sex：Area (male,female)
 		default:male
 	Age：Unit (Years)
 	Telephone：Home  Unit(number)
 			   mobile Unit (number)
 -------------------------------------------------------------
 教师框架
 Frame< Teachers >
 	AKO< Teachers-Students >
 	Major：Unit(Major-Name)
 	Lectures：Unit(Course-Name)
 	Field：Unit(Field-Name)
 	Project：Area(Nation,Provincial,Other)
 			default：Procincial
 	Paper：Area(SCI,EI,Core,General)
 			default：Core
 -------------------------------------------------------------
 学生框架
 Frame< Students >
 	AKO< Teachers-Students >
 	Major：Unit(Major-Name)
 	Classes：Unit(Classes-Name)
 	Degree：Area(doctor,master,bachelor)
 			default：bachelor

第3章确定性推理

将以下谓词提出为子句：

变成子句集的步骤

（1）（∀X）（∀Y）（p（x，y）∧Q（x，y））

它已经是标准类型，p（x，y）∧q（x，y）也是一个组合范式，它直接消除了全名量词和组合词

s = {p（x，y），q（x，y）}

（2）（∀X）（∀Y）（p（x，y） - > q（x，y）

=（∀x）（∀Y）（¬p（x，y）v q（x，y））

已经是Skolem标准

s = {¬p（x，y）v q（x，y）}

（3）（∀X）（∃Y）（p（x，y）v（q（x，y） - > r（x，y））））

=（∀x）（∃Y）（p（x，y）v（€q（x，y）v r（x，y）））））

消除存在量词，然后用y替换F（x）

=（∀x）（p（x，y）v q（x，f（x））v r（x，f（x）））

已经标准了

s = {p（x，y）v- q（x，f（x））v r（x，f（x））}

（4）（∀X）（∀Y）（∃Z）（p（x，y） - > q（x，y）v r（x，z））

=（∀X）（∀Y）（∃Z）（¬p（x，y）v q（x，y）v r（x，z））

消除存在量词，然后用f（x，y）替换z

=（∀x）（∀Y）（¬p（x，y）v q（x，y）v r（x，f（x，x，y）））

s = {€p（x，y）v q（x，y）v r（x，f（x，y））}

确定以下哪些条款不令人满意

（1）{¬pv q，¬q，p，¬p}

不满意意味着永久虚假

这是不令人满意的

（2）{p v q，梦，p v q，p v -q，¬pv -q}

这是不令人满意的

（3）{p（y）v q（y），¬p（f（x））v r（a）}

这不是不令人满意的，最终结果不是零

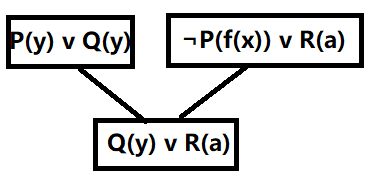
（4）{€p（x）v q（x），¬p（y）v r（y），p（a），s（a），¬s（z）v- v- v- r（z）}

不满意

（5）{¬p（x）v q（f（x），a），¬p（h（y））v q（f（h（y）），a）v-p（z）}

不满意

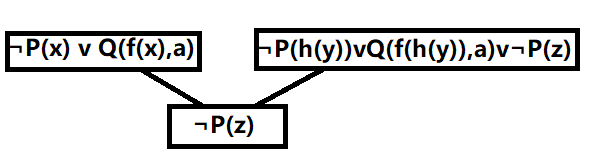
（6）{p（x）v q（x）v r（x），¬p（y）v r（y），€q（a），¬R（b）}

不满意

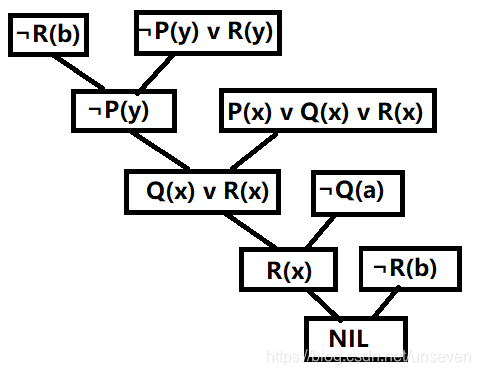
在以下问题上，证明G是否分别为F1，F2，…Fn的逻辑结论是

（1）

f：（∃x）（∃y）（p（x，y））

G：（∀Y）（∃X）（p（x，y））

首先，将f和f转换为子句集s。如果S减少到零，则表示G是F。

¬G：（∃Y）（∀X）（¬p（x，y））

s = {p（a，b），梦（x，b）}

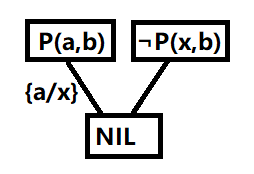
G是F

（2）

f：（∀x）（p（x）∧（q（a）v q（b）））

G：（∃X）（p（x）∧q（x））

¬G：（∀X）（¬p（x）v- q（x））

s = {p（x），q（a）v q（b），¬p（x）v- q（x）}

G是F

（3）

f：（∃x）（∃y）（p（f（x）∧Q（f（y）））

g：p（f（a））∧p（y）∧q（y）

¬g：¬p（f（a））v- p（y）v i q（y）

s = {p（f（m）），q（f（n）），梦（f（a））v- p（y）v- q（y）}

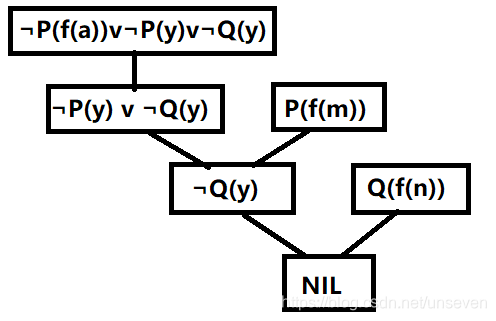
G是F

假设它是已知的

（1）如果X是Y，Y的父亲是Z的父亲，那么X是Z的祖父

（2）每个人都有父亲

证明使用锅炉演绎推理：对于某人，必须有一个人V，V是您的祖父。

首先定义谓词

f（x，y）：x是Y的父亲

GF（X，Z）：X是Z的祖父

p（x）：x是一个人

F1可以表示为：（∀x）（∀Y）（∀Z）（f（x，y）∧f（y，z） - > gf（x，z））

F2可以表示为：（∀Y）（∃X）（p（x） - > f（x，y））

g可以表示为：（∃U）（∃V）（p（u） - > gf（v，u）

将f1，f2，¬g制成子句集，s = {•f（x，y）v-（y，z）v gf gf（x，z），¬p（a）v f（x，x，y），

p（u），梦（v，u）}

假设张被盗，公共安全局派出五人进行调查。在案件分析期间，警员A说：“赵和Qianzhong的至少一个人犯下了犯罪。”警员B说：“ Qian和Sun Zhong的至少一个人犯下了罪行。”警员C说：“至少有一个来自太阳的人和利邦犯下了犯罪。”警员D说：“赵和阳股的至少一个人与案件无关。”警员E说：“至少有一个来自Qian和Lizhong的人与此案无关。”如果这五个侦察员都是可信的，请使用演绎推理来找出谁是小偷。

（1）首先定义谓词和常数

C（x）：表示X犯罪，z表示Zhao，Q表示金钱，S表示太阳，L表示Li

（2）在谓词公式中表达已知事物

Zhao和Qian的至少一个人犯下了犯罪：C（Z）V C（Q）

至少有一个钱和孙子犯下了犯罪：c（q）v c（s）

至少有一个来自太阳和李宗的人犯下了犯罪：c（s）v c（l）

至少有一个来自Zhao和Sun Zhong的人与案件无关：梦（z）

金钱和至少有一个人与案件无关：梦（q）v-（l）

（3）在谓词公式中表达所需的问题，并以否定为单位

如果犯罪者是u，则寻求的结论是c（u）。

有¬C（u）v c（u）

（4）以上扩展的条款集应根据结论的原则进行总结

金钱是囚犯，但显然仍然有几种条件未使用，因此可能有一个以上的囚犯。

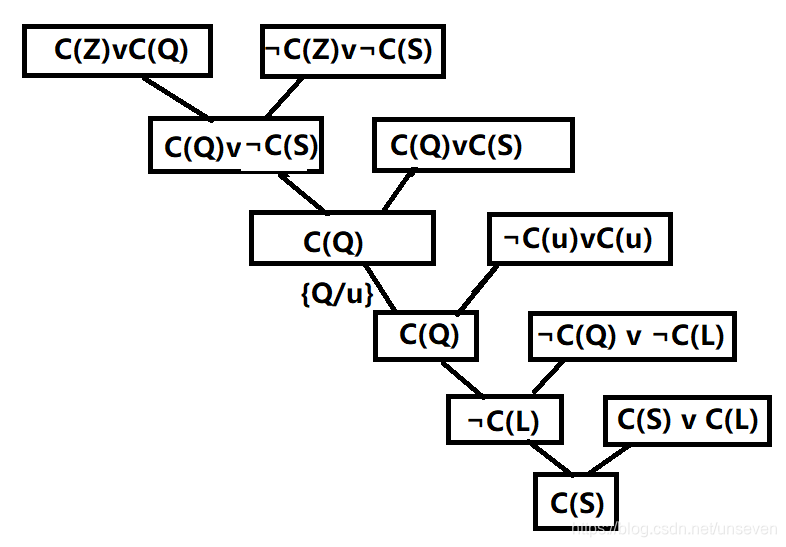
太阳也是囚犯

让我们提及单角质条款输入策略与线性输入策略之间的区别

单文本子句输入策略：要求参与结论的两个父子句中的至少一个是单文本子句。当子句集不满意时，使用此结论策略不一定会导致空白条款

线性输入策略：要求每次参加结论条款时，至少一个子句是初始子句集。简单有效但不完整。

考试1

1。多项选择问题

Al的英文缩写是（b）

A.自动智能

B.人工lntelligence

C.自动信息

D.人造信息

当精度的反转（溶解）证明了定理，如果当前精度为（c），则证明了定理。

A. Yongzhen风格

B.包含

C.空句

基于已知事实，通过规则基础获得结论的生产系统的推断方法是（a）

A.积极推理

B.反向推理

C.双向推理

当在语义网络中表达知识时，使用定向的Ako链和ISA链来表达节点知识（C）

答：非矛盾的

B.可伸缩性

C.继承

在继承的这一部分中，提到了Ako，ISA

（a→b）∧a=> b是（b）

A.其他法律

B.拒绝法

C.假推理

D.我们

命题可以通过真或错误来判断（d）

A.冲动

B.问题

C.句子

D.声明

量化各个变量的谓词称为（a）

A.一阶谓词

B.原子公式

C.二阶谓词

D.全名计

mgu是（a）

答：大多数

B.大多数一般替代品

C.最通用的谓词

大多数通用的统一机

1997年5月，在著名的“人机战争”中，计算机终于以3.5至2.5的总成绩击败了世界国际象棋Kasparov。这台计算机被称为（a）

A.深蓝色

B. IBM

C.深思熟虑

D.蓝天

人工智能系统知识的4个要素（D）不包括以下内容

A.事实

B.规则

C.控制和元知识

D.关系

或数字通常称为（d）

A.框架网络

B.语义图

C. Bo Yitu

D.状态图

不属于人工智能的学校是（b）

A.象征主义

B.机会主义

C.行为主义

D.连接主义

三所学校：象征主义，行为主义，联系主义

人工智能的含义是科学家在1950年首次提出的，他还提出了机器智能的测试模型。我可以问这个科学家（c）

A. Minsky

B. Zad

C.图灵

D.冯·诺伊曼

为了使机器聪明，有必要使机器知识。因此，人工智能中有一个研究领域，主要研究计算机如何自动获取知识和技能以实现自我完善。该研究分支称为（b）。

A.专家系统

B.机器学习

C.神经网络

D.模式识别

2。填写空白

不确定性类型分为：___随机性，模棱两可，不完整，不一致___。

In the process of deleting the policy, the following clauses are deleted: clauses with __ plain text, clauses with ___ eternal form, clauses with ___ __ clauses are concentrated in clauses with other clause classes.

规定了以下关系，以证明证据CF（a），CF（A1）和CF（A2）的可信度：

cf（〜a）= __- cf（a）__

cf（a1∧a2）= __ min {cf（a1），cf（a2）} __

cf（a1 v a2）= ___ max {cf（a1），cf（a2）} __

图：是指由__节点___和__指向边缘__组成的网络。根据连接相同节点的侧面之间的逻辑关系，可以将其分为___或Graph__和____和_____。

组合算法：找到具有相同谓词名称___的原子公式的___最通用组合（MGU）

在生产系统的推理过程中，从可触发的规则中选择一项规则。执行规则称为__触发规则___

p（b | a）指出，在规则_a-> b __中，在证据的作用下A是正确的，结论b是true__probability__

人工智能的长期目标是制造智能机器___

近期目标是实现机器智能________________________________

3。简短的答案问题